この論文では、現在デジタルコンピュータで一般的に使用されているデジタルプロッタの一種をコンピュータで制御するためのアルゴリズムについて説明します。1
1 この論文は、1963年8月30日にコロラド州デンバーで開催されたACM National Conferenceで著者が発表した「デジタルプロットのための増分アルゴリズム」に基づいています。
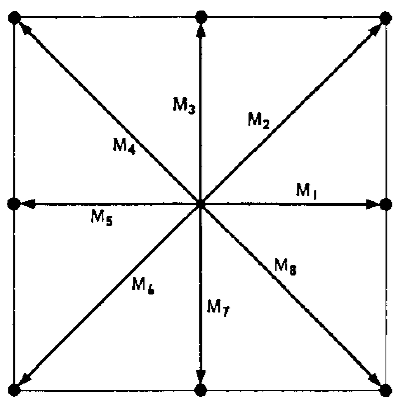
検討中のプロッタは、適切なパルスに応答して、図1に示す8つの直線動作のいずれかを実行することができます。したがって、プロッタはメッシュ上の点からメッシュ上の任意の隣接点まで直線的に移動できます。典型的なメッシュサイズは1/100インチです。

プロットされるデータは、メッシュに対してスケールされた \((x, y)\) 直交座標系で表現されます。つまり、データ点はメッシュ点上に配置され、結果として整数座標を持ちます。
図2に示すように、データには適切に選択された十分な数の点が含まれており、それらの点を線分で結ぶことで曲線を適切に表現できるものと仮定します。図3には、隣接する2つのデータ点 \(D_1(x_1, y_1)\) と \(D_2(x_2, y_2)\) を結ぶ線分がメッシュ上に拡大されて示されています。また、アルゴリズムに従ってプロッタが実際にたどる経路も示されています。各インスタンスにおいて、目的の線分に最も近いメッシュポイントが選択されます。例えば、\(Q\) は \(R\) よりも線分に近いため、\(D_1\) と \(D_2\) を結ぶ目的の線分を近似する際にプロッタがたどる経路の2番目のメッシュポイントとして \(Q\) が選択されます。

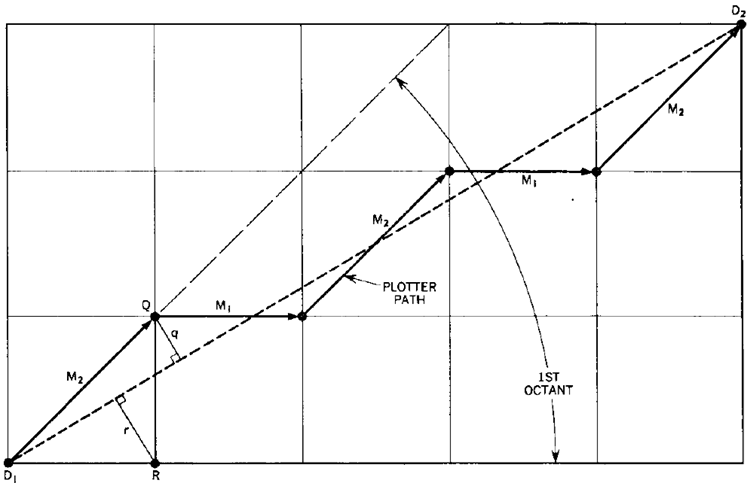
最初に検討するケースでは、原点を \(D_1\) へ移動させることによって得られる直交座標系において、\(D_2\) が第1八分円にあると仮定します。図3に示すように、プロッタの移動は \(M_1\) と \(M_2\) のみを含む一連の移動によって実現できることは明らかです。
図4は、原点を\(D_1\)に移動することで得られる\((a, b)\)座標系を示しています。したがって、\(D_2\)の新しい座標は\((\Delta a,\Delta b) = (x_2 - x_1, y_2 - y_1)\)となります。
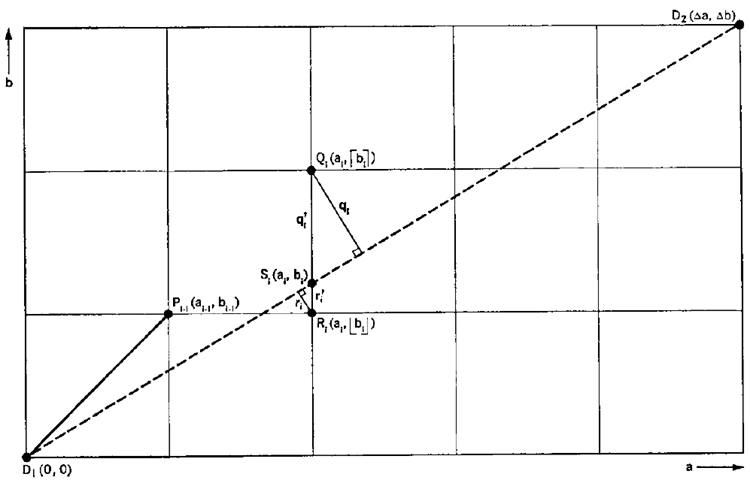
図4に示すように、プロッタが点\(P_{i-1}\)まで進むと、次の移動は、\(r_i \lt q_i\)の場合は\(M_i\)(点\(R_i\)へ)、\(r_i \geq q_i\)の場合は\(M_2\)(点\(Q_i\)へ)のいずれかになります。
相似三角形から、\(r_i^\prime — q_i^\prime\) は \(r_i - q_i\) と同じ符号を持つことがわかります。線分 \(D_1D_2\) は第1八分円内にあるため、\(\Delta a > 0\) となります。 したがって、\(\nabla_i = (r_i^\prime — q_i^\prime)\Delta a\) も \(r_i - q_i\) と同じ符号を持ち、適切な移動 (\(M_1\) または \(M_2\)) を選択する計算上の便宜のために使用できます。本論文の後半で、\(\nabla_i\) が以下の再帰関係を満たすことが示されます。 \[ \begin{align} \nabla_1 &= 2\Delta b - \Delta a \\ \\ \nabla_{i+1} &= \begin{cases} \begin{array}{l l l} \nabla_i + 2\Delta b - 2\Delta a & if & \nabla_i \geq 0 \\ \nabla_i + 2\Delta b & if & \nabla_i \lt 0 \\ \end{array} \end{cases} \end{align} \tag{1} \] ここで \[ \Delta a = x_2 - x_1, \Delta b = y_2 - y_1 \tag{2} \] (1)と(2)によって計算された\(\nabla_i\)の値は、プロッタの動きを決定するために使用されます。 \[ if \left\{ \begin{array}{l l l} \nabla_i \lt 0 & execute & m_1 \\ \nabla_i \geq 0 & execute & m_2 \end{array} \right\}\; i=1,\cdots,\Delta a \tag{3} \] ここで \[ m_1=M_1 and m_2 = M_2 \tag{4} \] 式(1)、(2)、(8)、(4)は、今回のケースのアルゴリズムを構成する。他の八分円の場合、式(2)と式(4)の各等式の右辺を修正する必要がある。
この修正を示す前に、再帰関係(1)が成り立つことを示す。図4で用いられている表記法は以下のとおりである。 \((a_{i-1},\hat{b}_{i-1})\)は\(P_{i-1}\)の座標を表すために用いられる。したがって、\(R_i\) と \(Q_i\) の座標はそれぞれ \((a_i, \lfloor b_i \rfloor)\) と \((a_i, \lceil b_i \rceil)\) となります。ここで、「\(\lfloor \; \rfloor\)」と「\(\lceil \; \rceil\)」は、床演算子と天井演算子を表すために使用されます。2 \(S_i\) の座標を \(b_i\) で表すと、\(S_i\) の座標は (\(a_i, b_i\)) となります。
2 floor演算子(\(\lfloor \; \rfloor\))とceil演算子(\(\lceil \; \rceil\))は次のように定義されます。\(\lfloor x \rfloor\)は\(x\)を超えない最大の整数を表し、\(\lceil x \rceil\)は\(x\)を超えない最小の整数を表します。この表記法はIversonによって導入されました。例えば、K. E. Iverson著「Programming notation in systems design」、IBM Systems Journal 2、117(1963年)を参照してください。
この表記法は \(\nabla_i\) の式を書き直すために使用されます。 \[ \nabla_i =(r_i^\prime — g_i^\prime)\Delta a = [(b_i - \lfloor b_i \rfloor) - (\lceil b_i \rceil - b_i)]\Delta a \] \(b_i = (\Delta b/\Delta a)a_i\) であることに注目すると、 \[ \nabla_i = 2a_i \Delta b - (\lfloor b_i \rfloor + \lceil b_i \rceil)\Delta a \] 線分 \(D_1D_2\) は第1八分円内にあるため、\(a_i = a_{i-1}+1\) です。 定義により、\(\lceil b_i \rceil = \hat{b}_{i-1}+ 1\) かつ \(\lfloor b_i \rfloor = \hat{b}_{i-1}\) です。これらの関係を用いて、\(\nabla_i\) について後者の式を、\(a_i\) と \(b_i\) を含まない形で書き直すことができます。 \[ \nabla_i = 2a_{i-1}\Delta b - 2\hat{b}_{i-1}\Delta a + 2\Delta b — \Delta a \] \(P_0, a_0 =0\) と \(\hat{b}_0 = 0\) の座標の初期条件を適用すると、 \[ \nabla_i = 2\Delta b - \Delta a \] \(\nabla_i \geq 0\)の場合、 \[ \hat{b}_i=\hat{b}_{i-1}+1 \] よって \[ \begin{align} \nabla_{i+1} &= 2(a_{i-1}+1)\Delta b-2(\hat{b}_{i-1}+1)\Delta a+2\Delta b-\Delta a \\ \\ &= \nabla_i + 2\Delta b - 2\Delta a \end{align} \] \(\nabla_i \lt 0\) の場合 \[ \hat{b}_i = \hat{b}_{i-1} \] よって \[ \begin{align} \nabla_{i+1} &= 2(a_{i-1}+1)\Delta b -2\hat{b}_i\Delta a + 2\Delta b -\Delta a \\ \\ &= \nabla_i + 2\Delta b \end{align} \] したがって(1)が成り立つことが示された。
2番目のデータ点は、最初のデータ点に対して最初の八分円にあると仮定されています。2番目のデータ点が別の八分円にある場合、図5に示すように、最初のデータ点を原点とする\((a, b)\)直交座標系が選択されますが、各軸は八分円ごとに個別に方向付けられます。プロッタの動きに関連する方向m、mも示されています。この情報は、\(m_1\)および\(m_2\)への割り当てとともに、表1の左側の列にまとめられています。このように、式(1)および(4)の変形は8つの八分円それぞれについて指定されており、読者は、前述の式(2)および(3)と併せて、それらが一般的な場合の正しい定式化を構成していることを確認できます。
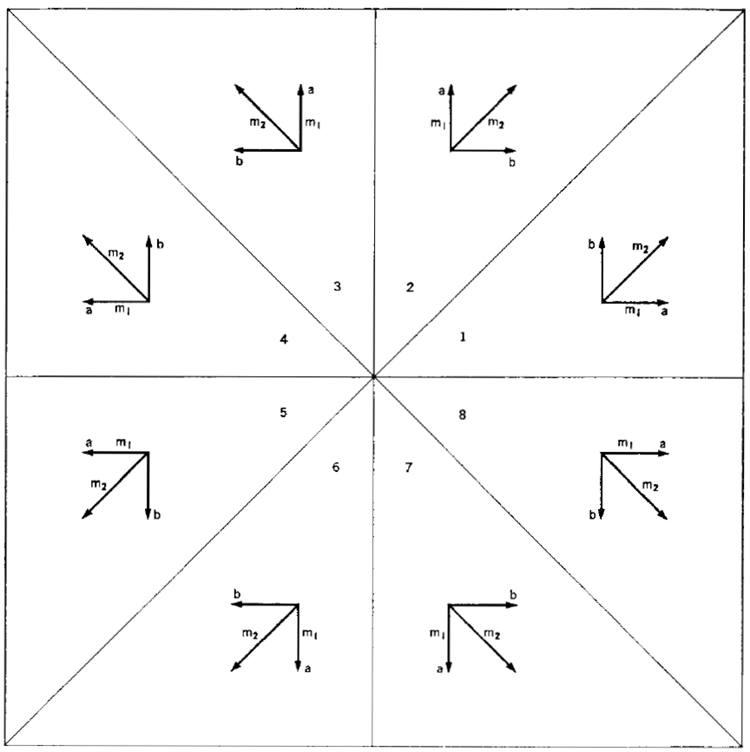
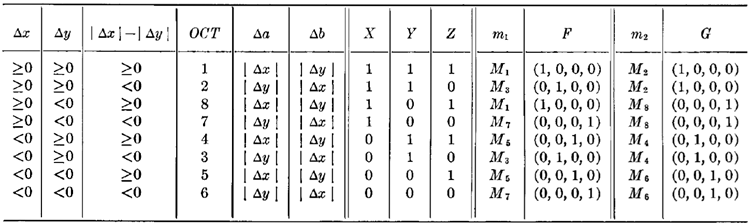
アルゴリズムを完成させるには、任意のデータ点のペアに適用可能な八分円を決定する計算手順が必要であり、それによって(2)と(4)の適切な形が決定されます。(2)の形は、\(|\Delta x| — |\Delta y|\)の符号に依存します。
(4) の形を求めるために、\(\Delta x, \Delta y,\) および \(|\Delta x| — |\Delta y|\) に対応するブール変数 \(X, Y,\) および \(Z,\) が導入される。表 1 に示すように、これらの変数は、対応する値が負であるかどうかに応じて 0 または 1 の値をとる。m, の割り当てを決定するために、関数 \[ F(X, Y, Z) = (XZ, Y\overline{Z}, \overline{X}Z, \overline{Y}\overline{Z}) \] 表1の考察によって発見された、Fに仮定された値とmの割り当てとの対応関係が導入される。\(F\)および\(m_1\)の列見出しによって、Fに仮定された値とmの割り当てとの対応関係が示される。同様に、 \[ G(X, Y) = (XY, \overline{X}Y, \overline{X}\overline{Y}, X\overline{Y}) \] は、表1の\(G\)列と\(m_2\)列と組み合わせて使用され、\(m_2\)への適切な割り当てが行われます。
このアルゴリズムは乗算や除算を使わずにプログラムできます。IBM 1401プログラム(IBM 1627の制御に使用)には、333個のコアロケーションで十分であることがわかりました。 連続するインクリメント間の平均計算時間は、約1.5ミリ秒でした。
3 F. G. Stockton, Algorithm 162, XMOVE PLOTTING, Communications
of the ACM 6, Number 4, April 1963. Certification appears in 6, Number 5,
May 1963.
4 F. G. Stockton, Plotting of Computer Output, Bulletin No. 139, California
Computer Products, May 1963.
著者の同僚であるD.クラークとA.ホフマンの提案は非常に役立ちました。